Advanced Exakt optimisation

Advanced information on Exakt setup

If the room into which the Exakt loudspeaker system is being installed is rather irregular in shape some further optimisation tricks may be applied.
Konfig provides information which will benefit an experienced installer and allow him to more quickly identify which mode filters will need to be adjusted, and in what way. To make use of this information it is useful to understand the limitations of the Konfig room mode calculation resulting from the assumptions made by the algorithms.
Presented in this section are the fundamental assumptions employed by the room mode optimisation algorithms. Advice for simplifying the dimensions when a room is not rectangular to those accepted by Konfig is given. Also recommendations for when to adjust the room mode filter centre frequency and bandwidth are presented.

Basic assumptions used for calculations of room modes

The optimisation algorithm assumes that the room is of essentially rectangular layout. This is often not the case. For Konfig to provide a meaningful room mode optimisation more complicated room shapes must be simplified to approximate rectangular dimensions. How the room is simplified will dictate the adjustment required to the Konfig optimisation.

The room mode algorithm also makes the assumption that the low frequency absorption (or transmission) of the walls, floor and ceiling are all approximately that of brick or cement block-work. When the room construction differs from this, or the walls contain large windows or multiple doors, some adjustment of the room mode gains will be required.

All reflections at room boundaries are considered to be specular. This implies that the reflective characteristics are ideal and are the same at all frequencies. Most real surfaces do not provide specular reflections, instead the magnitude and phase response of any reflected wave is dependent on the incident angle of the acoustic wave. This has significant implications for any non-axial mode (a mode which operates between more than two parallel surfaces).

Adjustment of room modes in Konfig

When a room mode filter is selected from the drop down list the user is provided with the full specification of the parametric equalising filter applied to optimise for the room mode. Any one of the three parameters (centre frequency, gain and bandwidth) may be adjusted to better optimise for a given room mode. The user is permitted to vary the filter gain by ± 100%, the centre frequency by ± 2 Hz and the bandwidth of the filter by ± 10%.

Additional information provided by Konfig

Konfig provides dimensional information about the room modes. The room mode filter titles shown on the drop down list also include a bracketed set of three characters. This describes the axis of the room along which the standing waves of the room mode occur.
Modes active along the length axis of the room are shown as [L--], those active across the width or height are shown as [-W-] and [--H] respectively.
The mode descriptor will also inform the installer whether a mode is a simple axial mode (operating along a single room dimension) or if the mode is tangential or oblique (operating between four or six room surfaces).

This is very useful information for the experienced installer. A length mode will be controlled by the characteristics of the front and rear walls. Say, for example, the front wall is made of glass; the installer will immediately know that any room mode indicated to operate along the length of the room will need to be adjusted. If the room has a pitched roof, any height mode will need to be adjusted.

Due to the non-ideal reflective characteristics of real surfaces any non-axial mode is likely to be over-optimised by Konfig. The installer will know that any mode described by more than one letter (e.g. [L-H] or [LW-]) is likely to require adjustment, typically an increase in filter gain (less cut).

Simplifying a room to rectangular dimensions

Presented hereafter are some examples of non-ideal rooms and how they should be simplified to fit the rectangular model employed by Konfig. In addition some recommendations are given for each room likely to improve the optimisation produced by the simplified rectangular model.

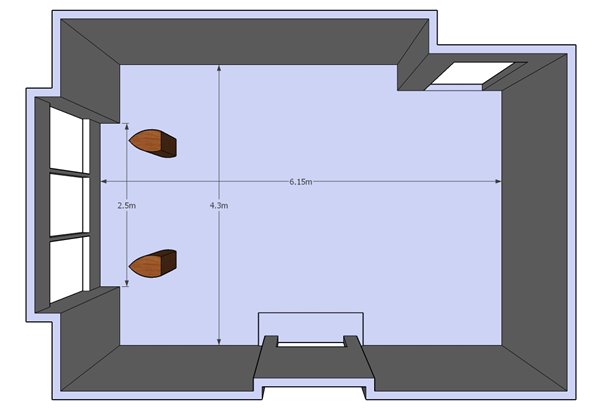
Example room 1, chimney breast and bay window

In general when measuring a room the dimension should be taken which corresponds to the largest parallel surface area of opposite walls. In the example below, the inset door and chimney breast (fireplace) account for less than 50% of the side walls so they are ignored and the measurement taken is to the most distant surfaces (4.3m). The bay window covers more than 50% of the end wall so the length of the room is measured into the window (6.15m).

The windows will allow sound energy to pass through rather than being reflected back into the room as would be the case for a solid wall. As the bay window forms a large part of the boundary for any length mode it is likely that all length modes will be over optimised by Konfig. While attention should be given to all Konfig calculated modes, particular attention to the gain applied to length modes is recommended. It is highly likely that the gain for length modes will need to be increased (less cut).

As the bay window along with the remainder of the front wall forms a staggered surface some smearing of room modes relating to the length of the room may occur. This can be countered by slightly increasing the bandwidth of any length modes.

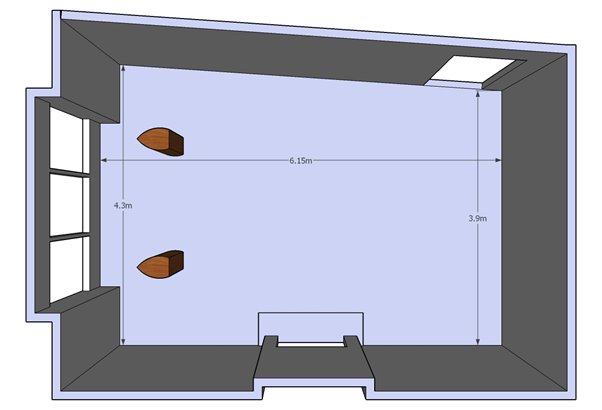
Example room 2, room with non-parallel walls

Where walls are angled it is recommended to take an average measurement. For the room below the length remains at 6.15, measured into the bay window. The width would be taken as 4.1m, the average width.

As with the previous example, it is likely that any length modes will need attention, especially with regard to the optimisation filter gains

Modes relating to the width of the room may also need attention. It is likely that the optimisation filter gain for width modes will need to be reduced as non-parallel walls will reduce the strength of any modal behaviour. It may also be beneficial to increase the bandwidth of any width modes to capture the spread of modal frequencies resulting from the non-parallel surfaces.

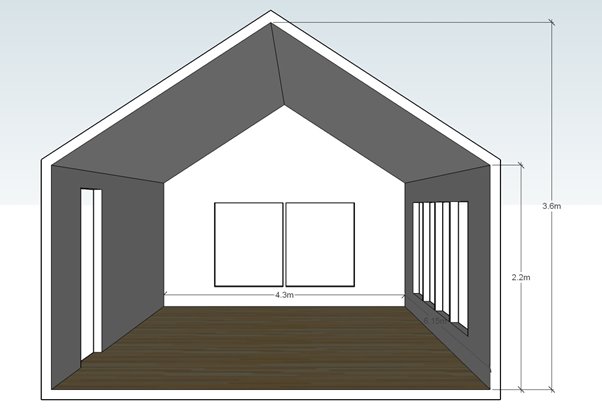
Example room 3, room with pitched roof

For a room with a pitched roof careful attention to any room modes operating in the vertical axis is required. The most reliable approach for optimising room modes where a pitched roof is present is to take the height measurement to approximately one third of the way up the pitched roof. The optimisation filter gain should be increased (less cut), and the bandwidth increased. For the example room below this corresponds to a height of 2.7m, an increase in bandwidth of any height modes of between 5% and 10%. The gain adjustment will depend on the construction type of the floor and ceiling, but is easily adjusted using the tune-dem.

As the floor plan of the room is a pure rectangle the width and length of the room are as given (4.3m and 6.15m). Due to the large window areas some reduction in the cut applied to length and width modes will be required.

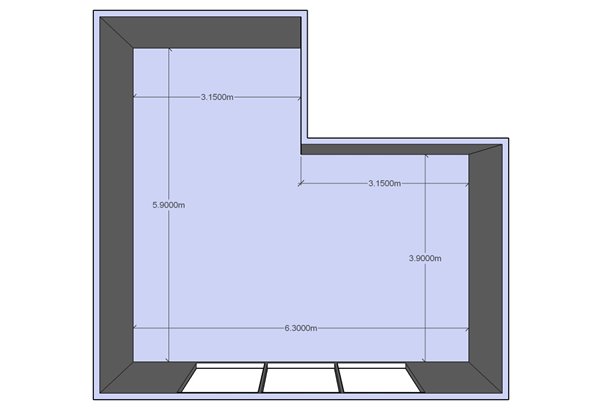
Example room 4, L-shaped.

A more challenging room shape to configure for room mode optimisation is an L-shaped room. The approach adopted will often depend on the location of the loudspeakers and listening position within the room.

The layout presented below presents quite a dilemma with regard to simplifying the room to a rectangular form. In this case the L-shape splits the room in half along the longest dimension. This makes it impossible to apply the approach where a dimension is dictated by the largest parallel surface of opposite walls (remember the bay window example). If the L-shape had split the room off-centre the choice of room dimensions would be simplified.

Taking the layout presented below, if the loudspeakers are placed centrally in front of the window facing into the room with the listening position also central, then obviously the width will be 6.3m. The length of the room could be given as 3.9m, 5.9m or somewhere in between. It is prudent to try both 5.9m and 3.9m room lengths in Konfig and using tune-dem decide which fits better. In my experience I have found using the shorter dimension, with a small decrease to the centre frequency, and small increase to bandwidth of any length modes to work quite effectively.

If the loudspeakers were placed against the right hand (3.9m) wall, it is likely that setting the room width to 3.9m (length will be 6.3m) will provide good results, as this width will be more vigorously excited by the loudspeakers.

If the loudspeakers were placed on the opposite (left hand) wall, firing along the 6.3m axis, it is likely that setting the width to 5.9m would provide better results.